元のURLがみれなくなっていた．webarchiveやstackoverflowに残っていたので写経しておく．

$\sin$関数は $$ \sin0 = 0 \\ \sin\frac{\pi}{2} = 1 \\ \sin\pi = 0 $$ となる．$\sin$関数の$0 \thicksim \pi$について着目する．この範囲を二次関数に近似してみる．
$$ y = a+bx+cx^2 $$ について $$ a+b\times0+c\times0^2=0\\ a+b\times\frac{\pi}{2}+c\times(\frac{\pi}{2})^2=1\\ a+b\times\pi+c\times\pi^2=0 $$ を満たす$a, b, c$は $$ a = 0\\ b = \frac{4}{\pi}\\ c = -\frac{4}{\pi^2} $$ となるので $$ \sin\theta \thickapprox \frac{4}{\pi}\theta-\frac{4}{\pi^2}{\theta}^2 $$ $\sin$は奇関数なので，入力が負の場合は符号を反転すればよい．

if(x > 0)
{
    y = 4/pi x - 4/pi^2 x^2;
}
else
{
    y = 4/pi x + 4/pi^2 x^2;
}

$\cos$は三角関数の周期性を利用する．$\cos\theta= \sin(\theta+\frac{\pi}{2})$として計算すればよい．$\frac{\pi}{2}$を加えて$\pi$以上になるのであれば$2\pi$を減算して範囲を$-\pi \thicksim \pi$に正規化して計算する．

x += pi/2;
 
if(x > pi)   // Original x > pi/2
{
    x -= 2 * pi;   // Wrap: cos(x) = cos(x - 2 pi)
}
 
y = sine(x);

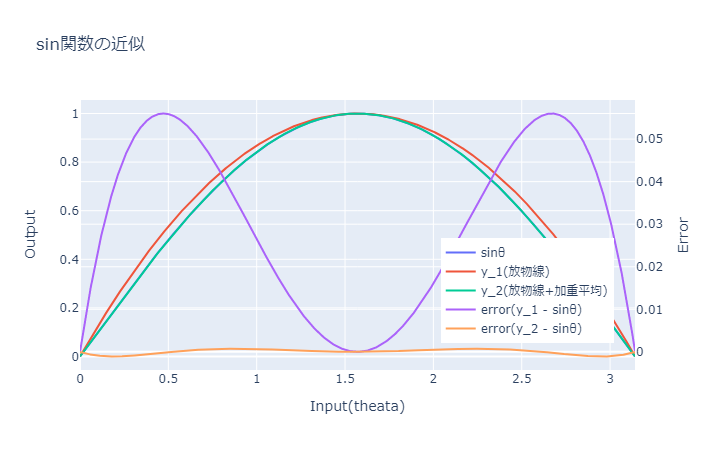
放物線近似による絶対最大誤差は0.056なので5.6%，用途によっては精度が十分かもしれないし足りないかもしれない．
グラフを書いてみると，$0, \frac{pi}{2}, \pi$を除いて近似が実際の$\sin$よりも大きい方をとっている．つまり，スケーリングすれば形状を近づけることができそう．2つの加重平均を利用してさらに近似する． $$ Q(\frac{4}{\pi}\theta-\frac{4}{\pi^2}{\theta}^2)+P(\frac{4}{\pi}\theta-\frac{4}{\pi^2}{\theta}^2) $$ ここで， $$ Q+P=1 $$ として，$Q$(と$P$）の値を設定することで，誤差を最小化できる．
絶対誤差を最小化 $$ Q = 0.775\\ P = 0.225 $$ 相対誤差を最小化 $$ Q = 0.782\\ P = 0.218 $$ ここでは絶対誤差の組み合わせを採用する．加重平均を加えた近似の最大誤差は0.001, 0.1%となり放物線のみの近似より50倍ほど精度が上がった．

最終的な実装

float sine(float x)
{
    const float B = 4/pi;
    const float C = -4/(pi*pi);
 
    float y = B * x + C * x * abs(x);
 
    #ifdef EXTRA_PRECISION
    //  const float Q = 0.775;
        const float P = 0.225;
 
        y = P * (y * abs(y) - y) + y;   // Q * y + P * y * abs(y)
    #endif
}

Fastest implementation of sine, cosine and square root in C++ (doesn't need to be much accurate)